Сюрпризы цикла

Выпишем в ряд элементы второго периода: Li Be В С N О F. Влево от среднего элемента периода углерода происходит увеличение металлических свойств элементов. Литий – типичный металл. При движении вправо увеличиваются металлоидные свойства. Фтор является типичным металлоидом. Очевидна зеркальная симметрия изменения химических свойств элементов относительности среднего элемента второго периода.

Аналогичная закономерность наблюдается и в других периодах. Выпишем в ряд часть элементов второго и третьего периодов: С N О F Nе Na Mg Al Si. От углерода к фтору происходит увеличение металлоидных свойств элементов, от кремния к натрию – металлических. Между периодами, таким образом, так же существует зеркальная симметрия динамики изменения, химических свойств элементов относительно инертного газа, их соединяющего.

С точки зрения нашей циклической структуры симметрия в периоде объясняется тем, что левая циклоида зеркально симметрична правой, а зеркальная симметрия между периодами – симметрией верхней (положительной) и нижней (отрицательной) циклоид.

Циклическая структура состоит из четырех циклов-кругооборотов. О чем же может поведать номер каждого цикла?

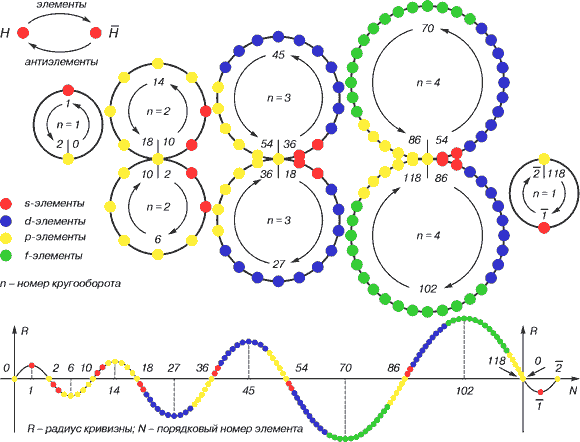
Рис. 3. Структуры времени и пространства в цикле водород – антиводород (обозначены начальные, средние и конечные элементы периодов)

Номер кругооборота определяет количество нейтронов, которое приходится на два протона в ядрах элементов.

В самом деле, при анализе зависимости числа протонов от числа нейтронов в ядрах элементов мы установили, что при увеличении на два протона в ядрах элементов первого кругооборота количество нейтронов увеличивается на один, во втором на два, в третьем на три, а в четвертом на четыре нейтрона.

Номер кругооборота определяет количество элементов в периодах.

В периодах – окружностях каждого цикла кругооборота находится следующее количество элементов: в первом – 2, во втором – 8, в третьем – 18, в четвертом – 32. Это количество элементов можно представить таким образом:

2·12, 2·22, 2·32, 2·42.

Или в общем виде через номер кругооборота 2n2. Мы видим, что количество элементов в периодах-окружностях равно удвоенному квадрату номера кругооборота.

Номер кругооборота определяют побочное и магнитное квантовые числа.

Мы установили, что число элементов в периодах-окружностях равно 2п2, где n – номер цикла-кругооборота. Из квантовой механики известно, что элементы в периодах не равноценны. Есть s-элементы, р, d и f. Такое деление обусловлено энергетическим состоянием электронов, которые находятся на внешнем электронном слое атома. Известно также их число, s-элементов два, р-элементов шесть, d – десять, f – четырнадцать. Можно ли это объяснить только на основе номера цикла-кругооборота?

Выпишем количество элементов на окружностях каждого оборота таким образом: первый кругооборот 2·1, второй 2·(1 + 3), третий 2·(1 + 3 + 5), четвертый 2·(1 + 3 + 5 + 7).

Налицо определенная закономерность: количество элементов равно удвоенному значению суммы последовательности нечетных чисел от 1 до 7. Следовательно, можно сказать, что первый кругооборот будет содержать один вид элементов (1), второй два (1 + 3), третий три (1 + 3 + 5), а четвертый четыре (1 + 3 + 5 + 7). Вполне понятно, что эти разновидности элементов отождествляются с s, р, d, f-элементами, то есть с побочным квантовым числом. В каждом виде элементов их содержится определенное количество, на это указывают цифры 1, 3, 5, 7, значит, эти цифры неявно отражают магнитное квантовое число.

Другое по теме

Как вселенная связана с электроном
В настоящее время точность физических констант, относящихся к электрону, уже достигла 10-9 - 10-12 [14]. Однако большинство данных, относящихся к Метагалактике, имеют неопределенность от одного до двух порядков величины. Такое большое различие в точности (на 10–13 порядков!) создает препятствие выявлению связей между к ...

Начала кондуктометрии
Кондуктометрия занимается изучением электропроводности растворов. В этой области электрохимии принято оперировать 2-мя характерными величинами: удельной электропроводностью (k - каппа) и эквивалентной электропроводностью (l ). Поясним физический смысл этих величин. Удельной электропроводностью называется электропро ...