Основные положения Специальной теории относительности

Пространство Минковского. Широко используемая в классической физике векторная форма записи законов природы объясняется не только желанием сэкономить место, но и является математическим отражением факта инвариантности законов природы относительно поворотов выбранной системы координат в пространстве, что, разумеется, требует инвариантной формы их математической записи. Действительно, в изображенных на рис. 12_1 повернутых друг относительно друга системах координат проекции всех векторов на одноименные оси различны, но равенство

(3)

справедливо в каждой из систем, т.е. остается инвариантным относительно пространственных вращений. Помимо равенств между векторами инвариантами являются скалярные произведения векторов и вычисляемые с их помощью квадраты длин:

(4) .

Координаты же вектора в новой системе отсчета могут быть рассчитаны через координаты в старой с помощью тригонометрии:

(5) .

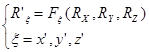Последовательное релятивистское описание явлений природы должно быть инвариантным относительно переходов из одной инерциальной системы отсчета в другую, движущуюся относительно первой. Как отмечалось, при таких переходах перестает быть справедливым классический векторный закон сложения скоростей, длина векторов изменяется, а в закон преобразований их компонент (преобразования Лоренца) помимо пространственных переменных входит время:

(6) .

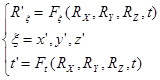В создавшейся ситуации естественным выходом был переход от несвязанных друг с другом пространственного (трехмерного) и временного (одномерного) описаний явлений к единому описанию событий в четырехмерном пространстве-времени (пространстве Минковского) при помощи четырехвекторов, три компоненты которых совпадают с обыконвенными простарнственными, а последняя дает временное описание. В этом пространстве переход в движущуюся систему отсчета рассматриваентся как обобщение понятия поворота, аналогом трехмерных траекторий являются четырехмерные кривые - мировые линии, инвариантами являются скалярные произведения четырехвекторо, определяемые соотношением:

(7) ,

и интервалы, являющиеся аналогами длин векторов:

(8)

(следствие преобразований Лоренца).

отличающимся знаками от обычного “трехмерного” определения. В связи с этим геометрическое свойства псевдоевклидового пространства Минковского существенно отличаются от привычных свойств евклидового пространства .

Световой конус.Мировыми линиями свтовых лучей, выходящих из одной точки пространства Минковского (т.е. одновременно испущенных из одной точки трехмероного пространства) являются прямые, составляющие с осью ct одинаковый угол и образующие световой конус (рис. 12_2) Мировые линии всех тел могут лежать лишь внутри светового конуса, поскольку допустимые скорости движения не могут превосходить с. Лежащие в верхней части светового конуса точки пространства Минковского образуют абсолютное будущее (множество событий, на которые в принципе можно повлиять, находясь в вершине конуса), нижняя часть светового конуса соответствует абсолютному прошлому (множество событий, которые в могли повлиять на происходящее в вершине конуса). Вне светового конуса лежат абсолютно недоступные событмя (т.е. невлияющие и независимые от происходящего в вершине конуса).

Другое по теме

Акпп - пользование, обслуживание, диагностика
Улучшение эксплуатационных качеств современного автомобиля привело к значительному усложнению его конструкции. А оснащение автомобилей автоматической трансмиссией позволило резко снизить объем нагрузки, возлагаемой на водителя во время движения, что также благоприятно отразилось на ходовой части, двигателе и скоростных ...

Эволюция и сотворение мира
Разница между учением Библии и естественнонаучным взглядом на возникновение мира и жизни на Земле состоит вовсе не в противопоставлении мгновенного возникновения и длительного развития. Согласно Книге Бытия Бог последовательно сотворил свет, твердь небесную, сушу и растительность, светила, рыб и птиц, животных и челове ...