Расчеты во фронтальной хроматографии

где

2x - объем пробы;

С 'max , s - высота и ширина пика, образованного объемом пробы 2x.

(Конечно, можно возразить тому, что количество вещества равно произведению высоты на ширину пика в условиях большого объема пробы, но об этом я предлагаю на время забыть. Если конечные выводы, основанные на этом предположении будут удовлетворительными, то и не стоит этими проблемами забивать голову! )

Предыдущая работа " Влияние объема пробы на хроматографический процесс" показала, что

s = 0,257(2x)2 +1.

Однако если быть откровенным, коэффициент 0,257 в формуле используется только для того, чтобы расширить рабочий интервал объема проб. На самом деле для небольших объемов проб коэффициент равен 0,235. Комбинируя (6) и (7) получим

Возвращаясь к выражению (5) мы получим функцию, описывающую фронтальную кривую:

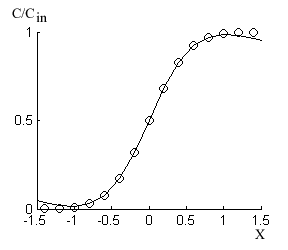
Сделав столь важный вывод, пора подумать о правомерности сделанных ранее допущений *). Иными словами, насколько полученная функция точно описывает фронтальную кривую. Проверить это несложно. Надо сравнить график, полученный решением функции (3) численным способом, и график новой функции. Результаты сравнения показаны на рисунке. В диапазоне x от -1 до 1 погрешность аппроксимации не превышает 0,5 10-2 Сin. Из этого следует, что новая функция удовлетворительно описывает 95% фронтальной кривой по высоте.

Однако нам предстоит решить главную задачу: как получить формулу для расчета эффективности хроматографической системы, исходя из данных фронтальной хроматографии.

Я буду исходить из своих личных достижений

N = 5,545 VrVmr / s0 2 ,

которые подробно изложены в предыдущей работе " Расчет эффективности хроматографических систем".

Что мы должны преобразовать в этой формуле, чтобы получить формулу для расчета эффективности для фронтальной хроматографии? Прежде всего, следует найти такой участок на фронтальной кривой, который был бы равен s0/(5,545)1/2 , так как этот шаг позволит ликвидировать коэффициент 5,545. Используя нашу новую формулу, несложно найти С/Сin при x= ±1/(5,545)1/2. Полученная величина составляет 0,159, поэтому

Подобного рода формул можно получить целое семейство. Например, на практике удобнее использовать формулу с (Vmr - V0,25):

Другое по теме

Пища с точки зрения химика
Минеральные вещества не обладают энергетической ценностью, как белки, жиры и углеводы. Однако без них жизнь человека невозможна. Особенно важна их роль в построении костной ткани. Минеральные вещества участвуют в важнейших обменных процессах организма: водно-солевом и кислотно-щелочном. Многие ферментативные процессы в ...

Метод стандартной добавки и метод Грана.
Перед тем, как излагать индивидуальные особенности той или иной разновидности метода добавок, опишем в нескольких словах процедуру анализа. Процедура состоит в том, что в анализируемую пробу делается добавка раствора, содержащего тот же анализируемый ион. Например, для определения содержания ионов натрия делаются добавки станд ...