Расчеты во фронтальной хроматографии

Я не могу утверждать, что фронтальная хроматография и сопутствующие ей расчеты часто используются в хроматографическом мире. Область применения фронтальной хроматографии ограничена обычно препаративными исследованиями. Однако непопулярность не означает ненужность!

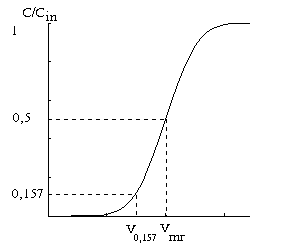
Для расчета эффективности хроматографических колонок, исходя из данных фронтальной хроматографии, обычно используется следующая формула:

Обозначения можно понять из рисунка.

У этого выражения есть один серьезный недостаток - нет связи с закономерностью перераспределения вещества в хроматографических системах при обычных условиях, т.е. при малом объеме пробы. Действительно, найти строгую логическую связь между следующими формулами довольно трудно:

Связь же должна быть, так как фронтальная хроматография является частным случаем хроматографии при обычных условиях. При таких рассуждениях логичнее бы выглядела формула

.

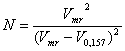Мои поиски в научной литературе ни к чему не привели. А если вышеупомянутой связи нет, то и ценность формулы (1) значительно снижается.

Для исправления создавшегося положения я предпринял определенные шаги, позволяющие вывести формулу, которая не противоречила бы общим хроматографическим воззрениям.

Так как для фронтальной хроматографии предполагается, что объем пробы неограниченно велик, то перемещение хроматографической зоны рассматривается как суммарный результат движения множества хроматографических пиков, образованных объемом одной пробы. При этом фронтальная кривая может быть описана следующим образом:

где

Сmax , s0 - высота и ширина хроматографического пика, полученного при объеме пробы, равном объему одной теоретической тарелки;

Vm - свободный объем колонки;

x - осевая координата, единица которой равна ширине пика на высоте Cmax/2 от основания.

Не вызывает сомнения, что Сmaxs0N/Vm=0,94Cin , так как произведение высоты пика на его ширину пропорционально величине концентрации исходной пробы. В связи с этим

Использовать это выражение на практике не представляется возможным, так как интеграл от функции Гаусса в неопределенном виде не решается! Выходом из положения может быть приближенное решение этой задачи. На пути решения не мешает сделать следующее преобразование:

Дальнейшие рассуждения будут несколько неожиданными!

Второе слагаемое при внимательном рассмотрении очень напоминает половину высоты пика при условии, что объем пробы составляет 2x. Что может дать нам это наблюдение? Оказывается, что много! Поскольку влияние объема на ширину пика было подробно изучено ранее в предыдущей работе, то высоту пика (Сисх) можно вычислить как результат деления количества вещества в пробе на ширину пика.

Другое по теме

Научное объяснение, его структура и основные разновидности. Предсказание
Объяснение – важнейшая функция чел познания, в частности научного исследования, состоящая в раскрытии сущности изучаемого объекта. В реальной практике исследования О. осуществяется путем показа того, что объясняемый объект подчиняется определенному закону. Теор познания различает структурные объяснения, отвеч на вопрос ...

Питание как важнейшая потребность человека
Эта работа создана с целью ознакомления читателя с основными моментами проблемы питания как важнейшего процесса, обеспечивающего существование всего живого на Земле, в том числе Homo Sapiens. В доступной и популярной форме излагаются важнейшие сведения о питательных веществах, их элементарной классификации и их физиолог ...