Определение диаметра труб дюкера ( для случая , когда работает только одна труба дюкера ) .

где - коэффициент гидравлического трения ; - длина трубы , м ; - диаметр поперечного сечения трубы , м .

Подставляем формулы ( 1.8 ) и ( 1.9 ) в выражение ( 1.7 ) , имеем :

( 1.10 )

Найдем значения местных коэффициентов сопротивления :

а) коэффициент сопротивления входной решетки ищем по формуле Киршмера :

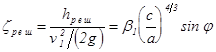, ( 1.11 )

где - средняя скорость перед решеткой , м/с ; - потеря напора решетки , м ; - коэффициент, принимаемый по таблице 4-22 /1, с.202/ , в зависимости от формы поперечного сечения стержней решетки ( принимаем тип стержней - №1 , соответствующее ему значение = 2.34 ) ; , - толщина стержней и ширина просвета между ними соответственно ( принимаем =1 ) ; - угол наклона стержней решетки к горизонту ( принимаем = 90° ) .

По формуле ( 1.11 ) получаем :

;

б) коэффициент сопротивления при резком повороте ищется по формуле :

, ( 1.12 )

где и - эмпирические коэффициенты , принимаемые по таблице 4-6 и 4-7 /1, с.196/ , в зависимости от угла поворота трубы ( для заданного в задании угла поворота трубы = 45° ,= 1.87 и = 0.17 ) .

По формуле ( 1.12 ) получаем :

;

в) коэффициент сопротивления выхода принимаем равным 1 :

.

Диаметрпоперечного сечения трубы находится графическим способом , поскольку от величинызависят : площадь живого сечения w ; коэффициент гидравлического трения , ReD )

( где - относительная шероховатость и число Рейнольдса ReD =v ( - кинематический коэффициент вязкости , м2/с )) , а также некоторые коэффициенты местных сопротивлений . График зависимости диаметра поперечного сечения трубы от известного произведения строится по результатам вычислений , выполненных в таблице 1.1 .

Таблица 1.1 “ Параметры трубопровода “

Другое по теме

Происхождение и развитие галактик и звезд
К началу нашего века границы разведанной Вселенной раздвинулись настолько, что включили в себя Галактику. Многие, если не все, думали тогда, что эта огромная звездная система и есть вся Вселенная в целом. Но вот в 20-е годы были построены новые крупные телескопы, и перед астрономами открылись совершенно неожиданные ...

Современная астрономия
Данный реферат посвящен современным вопросам астрономии - той области знаний, которые за последние годы дали наибольшее число научно-технических открытий. Вся история изучения Вселенной есть, в сущности, поиск средств, улучшающих человеческое зрение. До начала XVII века невооруженный глаз был единственным оптическим ...