Расчет элементов резервуара

Так как Ne = 940 кН > N = 247,5 кН проектом предусмотрено крепление щитов покрытия к каркасу и стойке резервуара. Окаймляющие щиты уголки привариваются к каркасу угловыми швами с катетом Кf = 6 мм, а к оголовку (зонту) стойки каждый щит закрепляется временным болтом М16 с последующей приваркой его к кольцу стойки. Обшивки смежных щитов покрытия соединяются на монтаже по всей длине угловыми швами Кf = 25 мм.

Общая нагрузка от веса резервуара без учета нагрузки от веса днища Jc = 722,8 кН (лист 4 [4]).

Усилие, отрывающее корпус от днища

Проверяем напряжения в швах, прикрепляющих нижний пояс стенки к днищу, при действии усилия отрыва

где

Rwf — расчетное сопротивление угловых швов срезу (условному) по металлу шва (табл. 56 [2]);

βf = 0,7 — коэффициент для ручной сварки, принимаемый по табл. 34* [2].

Стойка приваривается к днищу по контуру опорного кольца.

Пригрузка стойки производится путем обетонирования ее по контуру опорного ребра на высоту 1,5 м. Объем бетона 8,3 м3, вес пригруза 19,3 т.

4.5. Проверка устойчивости корпуса резервуара при совместном действии вертикальных и горизонтальных (боковых) сжимающих усилий выполняем согласно рекомендациям п. 8.5 … 8.9 [3] по формуле

где σ1 и σ2 — соответственно абсолютные значения расчетных продольных и кольцевого сжимающих напряжений;

σcr1 и σcr2 — соответственно критические напряжения при раздельном равномерном действии осевого и радиального сжатия;

γс = 1.

Проверяем устойчивость формы резервуара для четвертого пояса, где t = 6 мм.

Продольное и кольцевое сжимающие напряжения в элементе 949 (приложение 2) от постоянной, снеговой нагрузок и вакуума (загружения 1, 4, 5) соответственно равны σ1 = 1,41 МПа и σ2 = 0,5 МПа.

Определяем критические напряжения по пп. 8.5 и 8.7 [3].При равномерном сжатии вдоль образующей цилиндрической оболочки σcr1 принимается равной меньшей из величин.

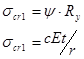
где ψ, с — коэффициенты, принимаемые по п. 8.5 [3].

При r/t = 1140/0,6 = 1900 > 300 коэффициент ψ не учитывается, а коэффициент

с = 0,066 (по интерполяции).

Тогда

При Н/r = 12/11,4 = 1,05 σcr2 определяем по формуле

Проверяем устойчивость по формуле

т.е. устойчивость корпуса обеспечена.

Другое по теме

Антропный космологический принцип
Идеи антропного космологического принципа, развивавшиеся в последнем столетии XX века, представляют большой научный интерес с точки зрения ответа на вопросы происхождения и эволюции окружающего мира. Основная идея этого принципа состоит в том, что фундаментальные свойства Вселенной, значения основных физических констант ...

Проблема происхождения и эволюции человека
Проблема происхождения и эволюции человека занимает умы людей на протяжении многих веков. Существует множество теорий появления человека на Земле. В настоящее время большинство ученых склоняется к происхождению человека в результате эволюции и естественного отбора от высокоразвитых предков современных обезьян. Так к ...