Операторы.

В начале 20 века в математике были введены новые объекты - операторы, без использования которых современная физика была бы немыслима. Понятие оператора является естественным обобщением традиционного для классической математики понятия функции. Если под функцией понимается закон (правило, отображение), по которому одному числу (набору чисел) ставится в соответствие другое число (набор чисел), то под оператором подразумевают закон, по которому одному объекту (группе объектов) ставится в соответствие другой объект (группа). Наиболее часто встречаются операторы, действующие на функции (операторы умножения на число, дифференцирования, интегрирования и т.д.) или векторы (оператор поворота, проектирования и т.д.). Весьма полезной оказалась идея определения математических операций над операторами. Например, под произведением двух операторов подразумевается оператор, выполняющий последовательно действия каждого из перемножаемых операторов. Для операции умножения операторов в общем случае не выполняется свойство коммутативности:

(5) .

Использование языка операторов существенно сокращает запись многих математических формул и делает их более “элегантными”. Так введение лишь одного дифференциального оператора “набла”

при помощи стандартным образом определенных операций скалярного ( , ) и векторного [ , ] умножения позволяет записать системы уравнений (3) и (4) в весьма компактной форме:

(3’) ;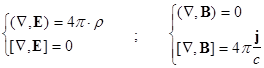

(4’) , .

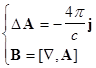В последних равенствах использован оператор Лапласа:

(7) .

Помимо краткости записи преимущество операторного метода состоит в том, что. с самим оператором набла можно обращаться почти так же, как с обычным вектором, что, несомненно, облегчает громоздкие выкладки.

Другое по теме

Возможности использования анализатора жидкости Флюорат 02-3м для анализа питьевой и природной воды
Государственное унитарное предприятие "Центр исследования и контроля воды", осуществляющее регулярный контроль питьевых и сточных вод предприятий Санкт-Петербурга, имеет многолетний опыт разработки методик выполнения измерений и испытания средств измерения. В последние годы Центр исследования и контроля воды ...

Непредельные, или ненасыщенные, углеводороды ряда этилена (алкены, или олефины)
Алкены, или олефины (от лат. olefiant - масло — старое название, но широко используемое в химической литературе. Поводом к такому названию послужил хлористый этилен, полученный в XVIII столетии, — жидкое маслянист вещество.) — алифатические непредельные углеводороды, в молекулах которых между углеродными атомами имеется ...