Непрерывные распределения зарядов.

Входящие в выражения для электростатических и магнитостатических полей (9_4) и (9_8) суммы в случае макроскопических заряженных тел содержат очень большое число слагаемых, соответствующих вкладам в поля от точечных зарядов. Их вычисление неудобно с чисто “технической” точки зрения: математическая операция суммирования более трудоемка, чем, например, интегрирование (сказанное относится к аналитическим расчетам, при компьютерном счете суммирование предпочтительнее взятия интегралов, однако в 19 веке подобной альтернативы в математике не существовало). Переход к интегрированию требовал приближенной замены дискретного распределения элементарных зарядов на непрерывное, характеризуемое плотностью электрического заряда (отношение величины заряда к объему содержащего его небольшого, но макроскопического элемента пространства):

(1) .

Естественно, что замена (1) приводила к “сглаживанию” рассчитываемых макроскопических полей по сравнению с реальными микроскопическими, сильно изменяющимися на сравнимых с размером атома расстояниях. Описанный переход к непрерывному распределение зарядов существенно упрощал расчеты, не снижая их практическую ценность (наука и техника 19 века еще не доросли до эффектов, происходящих на микроскопическом уровне организации материи).

Математический формализм. Переход к непрерывным распределениям зарядов и токов позволил переписать законы электро и магнитостатики сразу в нескольких математических формах, эквивалентных по физическому смыслу, но существенно различающихся по технике выполнения конкретных расчетов:

интегральные формулировки:

;

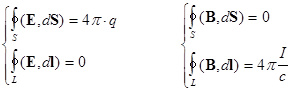дифференциальные формулировки:

(3) ;

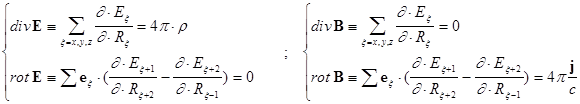расчет полей через скалярный и векторный потенциалы:

.

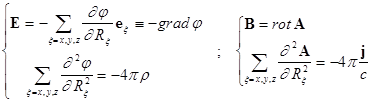Т.о. адекватное описание одних и тех же законов естествознания возможно на различных языках математики.

Другое по теме

Современная астрономия
Данный реферат посвящен современным вопросам астрономии - той области знаний, которые за последние годы дали наибольшее число научно-технических открытий. Вся история изучения Вселенной есть, в сущности, поиск средств, улучшающих человеческое зрение. До начала XVII века невооруженный глаз был единственным оптическим ...

Метод стандартной добавки и метод Грана.
Перед тем, как излагать индивидуальные особенности той или иной разновидности метода добавок, опишем в нескольких словах процедуру анализа. Процедура состоит в том, что в анализируемую пробу делается добавка раствора, содержащего тот же анализируемый ион. Например, для определения содержания ионов натрия делаются добавки станд ...