Связь естественных единиц длины, массы, времени с константами электрона.

М. Планк на основе констант G, c ,h получил естественные единицы длины, массы, времени. М.П. Бронштейн использовал фундаментальные константы для исследования взаимосвязи физических теорий на основе констант G,c,h [2]. А.Л. Зельманов сделал геометрическое обобщение идей Бронштейна и построил куб физических теорий [2]. На основе фундаментальных констант G,c,h предпринимаются попытки построить квантовую теорию гравитации, выбирая в качестве естественных единиц планковские константы. Эта задача еще не решена. Возможно причина состоит в том, что планковские константы не являются минимальными единицами длины, массы, времени. В.И. Вавилов еще в 1934 году высказал мысль о том, что было бы важно установить целый ряд естественных единиц, охватывающих процессы разных масштабов [4].

Для этой цели можно продолжить исследование вариантов построения куба физических теорий на основе геометрического обобщения А.Л. Зельманов, используя другие комбинации констант. В частности, можно построить гиперкуб на основе четырех констант. Такой подход был предпринят в [7], что позволило получить новые естественные единицы длины, массы, времени.

В [1,3,5,6] показано, что три константы не могут составлять полный константный базис физической теории. Не является полным и 4-х константный базис. Поэтому возможности 3-х мерного куба А.Л. Зельманова и 4-х мерного гиперкуба для исследования физических теорий имеют ограничения. Для построения физической теории минимальное количество констант должно быть равно пяти [3]. В связи с этим геометрическое обобщение, обладающее полнотой, должно включать пять измерений. Это значит, что от 4-х мерного гиперкуба необходимо перейти к 5-ти мерному суперкубу. Если построить 5-ти мерный суперкуб, основанный на пяти константах, то он будет иметь вид, приведенный на рис.1.

Рассмотрим суперкуб (рис. 1) на основе пяти универсальных физических суперконстант hu, lu, tu, α, α2 [1,3-7].

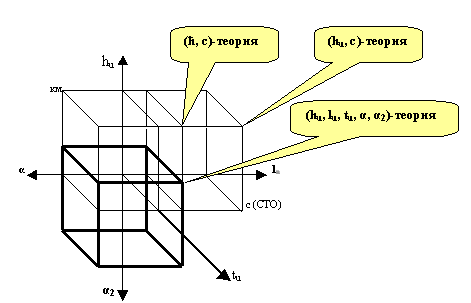
Рис.1. Суперкуб (hu, lu, tu, α, α2)-пространства теоретической физики.

Этот суперкуб образован двойным смещением исходного (hu, lu, tu )-куба по координатам α и α2. Таким образом, первый след суперкуба представляет собой куб hu, lu, tu. Второй след суперкуба представляет собой гиперкуб hu, lu, tu, α.

Используя в качестве основных единиц константы hu, lu, tu, α, α2 получим такие единицы длины, массы, времени:

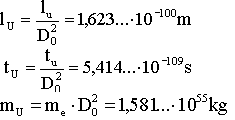
В приведенных формулах, D0 – большое число, значение которого определяется безразмерными суперконстантами α и α2 [3,5,6]. Обратим здесь внимание на то, что значение mU совпадает со значением массы Метагалактики с учетом темной материи. Как видим, эти единицы выражаются посредством констант электрона. Исследования различных систем естественных единиц показали, что системы естественных единиц легко представимы посредством констант электрона. В табл. 2 приведены соотношения, которые подтверждают это. Оказалось, что все системы естественных единиц, полученные разными авторами, можно представить новыми формулами с помощью констант электрона.

Табл. 2

Другое по теме

Основы обратноосмотической обработки воды
Метод обратного осмоса заключается в фильтрации растворов под давлением через специальные полупроницаемые мембраны, пропускающие молекулы растворителя и полностью или частично задерживающие молекулы либо ионы растворенных веществ. В основе метода лежит явление осмоса – самопроизвольного перехода воды через полупроницаем ...

Программа вступительных экзаменов по биологии в 2004г. (МГУ)
На экзамене по биологии поступающий в высшее учебное заведение должен показать: знание главнейших понятий, закономерностей и законов, касающихся строения, жизни и развития растительного, животного и человеческого организмов, развития живой природы; знание строения и жизни растений, животных, человека, основных ...