Стационарные состояния квантово-механических систем.

,

другие ортогональные линейные комбинации дают систему из близкорасположенных друг к другу N энергетических подуровней. При увеличении числа атомов в кристалле подуровни сливаются в сплошную полосу - энергетическую зону, соответствующую непрерывному набору разрешенных значений энергии электрона. Поскольку свободная частица в пустом пространстве так же может обладать энергией из непрерывного набора, поведение электрона в идеальном бесконечном кристалле весьма сходно с поведением свободной частицы. Этим объясняется возможность существования электропроводности в твердых кристаллических телах.

Уравнение Шредингера. При описании движения микрочастиц в пространстве в качестве базисного удобно выбрать непрерывный набор состояний с определенными координатами , для каждого из которых может быть записано уравнение, аналогичное (10). Конкретный вид оператора Гамильтона для этого случая был правильно угадан Шредингером и имеет вид, аналогичный классическому выражению для механической энергии:

,

где - оператор импульса, - оператор потенциальной энергии. Наибольший практический интерес представляют вероятности обнаружить находящуюся в стационарном состоянии частицу в заданной точке пространства R. В соответствии с общими правилами квантовой механики эта вероятность дается квадратом модуля соответствующей амплитуды, называемой волновой функцией:

.

Анализ математических свойств стационарного уравнения Шредингера

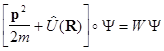
показывает, что в случаях, когда область классически возможного движения частицы в пространстве ограничена, разрешенным является только дискретный набор энергетических уровней. При неограниченном движении энергетический спектр непрерывен.

В простейшем случае стационарных решений для атома водорода связанным состояниям (электрон находится вблизи ядра) соответствует набор разрешенных значений энергии, полностью совпадающий с вычисленными в рамках первой модели Бора и прекрасно согласующийся с экспериментом (рис. 20_7). В ионизованном состоянии (электрон ушел от ядра на бесконечно большое расстояние) частица может обладать любым значением энергии.

Другое по теме

Одноатомные непредельные спирты (алкенолы и алкинолы)
Непредельные спирты (алкенолы и алкинолы) — производные непредельных углеводородов, в молекулах которых водородный атом замещен на гидроксильную группу. ...

Закон вечности
Природа имеет всеобщий и абсолютный ритм. Этот ритм равен семи. Коль скоро это так, то тогда, описывая математически циклическую структуру периодической системы, можно вывести своеобразный мировой закон. Периодическая система химических элементов, как известно, начинается с водорода. А существует ли конечный элемент, и ...