Векторные и скалярные величины.

C математической точки зрения вектором можно называть упорядоченный набор чисел лишь в том случае, если он обладает рядом определенных свойств. В частности, для любых двух таких наборов должны быть определены операции сложения и умножения на число так, чтобы выполнялись следующие свойства:

коммутативности:

(7) , ,

ассоциативности:

(8) , ,

и дистрибутивности:

(9) , ,

Поскольку свойства (7-9) справедливы для операций сложения и умножения вещественных чисел, практически все утверждения из алгебры скалярных величин остаются справедливыми и для векторов. Вектор является обобщением понятия числа на случай многомерных пространств. Скаляры можно рассматривать как векторы в одномерном пространстве.

Использование векторов позволяет строить описание весьма разнообразных объектов (материальных точек, сил, полей, состояний, численности населения городов, физиологических ощущений и т.д.), используя единообразные математические обозначения

Пользуясь аналогией с соотношениями (1-6), легко определить понятие вектора скорости изменения системы:

(10)

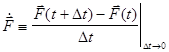
и обобщить все последующие соотношения на многомерный случай.

Движение материальной точки в пространстве трех измерений является частным примеров эволюции во времени весьма простой системы, исчерпывающее описание которой дается тремя декартовыми координатами, совокупность которых называется радиус-вектором:

(11)

(для обозначения “обычных” векторов в трехмерном пространстве будут использоваться жирные буквы без стрелок).

Сумма векторов определяется как вектор, составляющие которого являются суммами соответствующих составляющих слагаемых

(12) ,

а произведение на число - как вектор, составляющие которого получаются домножением составляющих исходного на это число:

(13) .

Легко убедиться, что все необходимые свойства (7-9) при таком определении операций выполняются. Производная радиус-вектора по времени получила название вектора мгновенной скорости:

(14) ,

а производная скорости - ускорения:

(15) .

По известной зависимости положения тела от времени R(t) его скорость и ускорение определяются однозначно. В случае заданной скорости V(t) для однозначного определения радиус-вектора R(t) необходимо знать положение тела в какой-то определенный момент времени (“начальное положение”). Если же задана зависимость ускорения от времени, то по ней может быть найдена скорость, а по последней - радиус-вектор. Очевидно, что решение будет однозначным, если заданы начальная скорость и положение тела.

Другое по теме

Некоторые выводы теории тяготения Эйнштейна
Ряд выводов теории Эйнштейна качественно отличается от выводов ньютоновской теории тяготения Важнейшие из них связаны с возникновением «черных дыр», сингулярностей пространства-времени (мест, где формально, согласно теории, обрывается существование частиц и полей в обычной, известной нам форме) и существованием гравитационных в ...

Метод двойной стандартной добавки.
Метод заключается в том, что к анализируемому раствору добавляются 2 порции стандартного раствора. Величина этих порций одинакова. По результатам измерений вычисляется параметр R = D E2 / D E1 , где D E1 - разность между потенциалом электродов в анализируемом растворе, и в растворе после первой добавки; D E2 - разност ...