Уравнение Дирака.

Предложенное П.Дираком уравнение является обобщением уравнения Паули на случай движения заряженных частиц со спином 1/2 с релятивистскими скоростями. К его конкретному виду можно прийти на основе сопоставления уравнений Шредингера, Клайна-Гордона и Паули:

------------------------------------------------------------------------------------------------------------------------------

********* Спин не учитывается Учет наличия спина

------------------------------------------------------------------------------------------------------------------------------

Нерелятивистская теория

(уравнение Шредингера) (Уравнение Паули)

------------------------------------------------------------------------------------------------------------------------------

Релятивистская теория

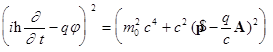
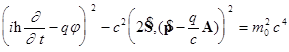
(уравнение Клейна-Гордона) (Уравнение Дирака)

------------------------------------------------------------------------------------------------------------------------------

Для сокращения записи уравнения приведены в операторном виде: сами волновые функции отсутствуют (напомним, что содержащие оператор спина уравнения в правом столбце таблицы подразумевают наличие двух компонент у волновых функций).

С точки зрения математики уравнение Дирака является дифференциальным уравнением второго порядка в частных производных. Чисто тождественными преобразованиями оно может быть сведено к системе из двух уравнений первого порядка. Последние можно объединить в одно уравнение первого порядка, связывающее четырехкомпонентные волновые функции. Релятивистское обобщение уравнения Паули приводит к необходимости допустить существование четырех допустимых внутренних состояний электрона вместо двух, постулируемых в классической теории.

Уравнение Дирака дает правильное количественное описание таких “тонких” эффектов атомно-молекулярной физики, как спин-орбитальное взаимодействие и позволяет верно рассчитывать поправки к энергиям атомных уровней, обусловленные релятивистской зависимостью массы от скорости. Написанные по аналогии с решением задачи для электрона выражения для описания магнитного взаимодействия ядра с электронами (изначально ниоткуда не следует, что тяжелые частицы, составляющие ядро должны подчиняться тем же уравнения, что и электроны) дают правильное описание сверх тонкой структуры спектральных линий. Уравнение Дирака подчиняется принципу соответствия: его разложение в ряд по малому параметру

(3)

(“постоянная тонкой структуры”) в нулевом приближении приводит к уравнению Шредингера, а в первом - к уравнению Паули.

Помимо успешного объяснения известных из экспериментов фактов уравнение Дирака предсказывало ряд неизвестных в то время эффектов, весьма странных даже с точки зрения квантовой механики.

Дираковский вакуум. Наличие четырехкомпонентной волновой функции в уравнении Дирака означало возможность четырех различных состояний свободного электрона в заданной точке пространства, два из которых интерпретировались как различные ориентации спина. С другой стороны, записанное для свободной частицы уравнение предсказывало возможность двух отличающихся знаком значений энергии:

Другое по теме

Производство бетонных работ при строительстве гидротехниче-ских сооружений
В комплексе работ по возведению гидротехнических сооружений основную часть составляют бетонные. Для их качественного выполнения требуется учитывать разнообразные условия и выбирать наиболее эффективные способы ведения. Бетонные работы включают в себя набор производственных процессов, позволяющих получить бетонную кладк ...

O Л. В. Канторовиче и линейном программировании
Я хочу написать о том, что я помню и знаю о деятельности Леонида Витальевича Канторовича, выдающегося ученого ХХ века, о его борьбе за признание своих экономико-математических теорий, о начальном этапе истории линейного программирования, о зарождении новой области математической деятельности, связанной с экономическими ...